�L���q�z�b�t�̖@�����T���Ƃ��낶��Ȃ�
�d�C�����n�߂��l�A���A���w���Ȑl�ɂƂ��ĂقƂ�ǂ̐l���ŏ����T���|�C���g���Ă����̂��A
�g�L���q�z�b�t�̖@���h
�Ȃ�ł���ˁB
���N�A�d���R����̃T�|�[�g�����Ă܂����}�W�ő����ł��B
����A���m�ɂ͑��������A�ł��B
�l���T�|�[�g������ɂ͉����@����Ă���̂ŁA�l�̎���ł͏��Ȃ��Ȃ�܂������A����ł��삯�o���̍��̓}�W�ő��������ł���B
�ŁA���̃T�C�g�������ɂȂ��Ă�����ł��A�����������͑����Ǝv���܂��B
�����āA���ʂ̎Q�l���ŁA���ʂɓƊw�ŕ����Ă���A����ς�����Ɠ���ł�����ˁB
�ł��l�͓����Ɏv����ł��B
�u�L���q�z�b�t�������B�B�B�v
�ƁB�i�j
�Ȃ�ł����Ă����ƁA���ۘb�����Ă݂�ƁA
�T���Ă�̂��āu�L���q�z�b�t�̖@���v�ł͂Ȃ��A�P�ɘA���������������Ȃ��A���Ă��������̎����قƂ�ǂȂ�ł���ˁB
�@���̓��e���̂͗������Ă���i�Ƃ����������ł��Ȃ��͂����Ȃ����x���j���A���̖@�����g���Đ����𗧂Ă���A���Ă������������Ă������Ă����i�K���T���Ă��邾���Ȃ̂ŁA
�����ł́A���̕ӂ��܂߂ĉ�����Ă����܂��B
�L���q�z�b�t�̑��@���͒��ȒP
�L���q�z�b�t�̖@�����āA���Ƒ��@��������܂����ǁA
���@���ł́A
�g����_�ɗ��ꍞ�ޓd���̑��a�Ɨ���o��d���̑��a���������h
�ƌ����Ă��邾���ŁA�߂�����ȒP�ł���ˁH
�d�C��H�̕���_�ł́A
���ꍞ�ޓd�� �� ����o��d��
�K�������Ȃ�܂���A�Ƃ��������̂��ƁB
����_�ɁAI�Ƃ�����{�̓d�������ꍞ��ŁA
I1��I2�Ƃ�����{�̓d��������o�Ă���A
���ꍞ�ޓd�� �� ����o��d��
I��I1+I2
�Ƃ������ƂɂȂ�B
I1��I2��I3�̎O�{�����ꍞ��ŁAI4��I5�Ƃ�����{������o�Ă���A
I1+I2+I3��I4+I4
�ɂȂ�B���ꂾ���B
���ꎩ�̂͂������ȒP�B
�L���q�z�b�t�̑��@�������͒��ȒP�ȂI
�����āA���@�����T���l�����Ƃ��܂����A���͂߂�����ȒP�Ƃ������A������O�̎��������Ă��邾���ŁA
�g�d�C��H�̔C�ӂ̈���̕����o�H�ɂ��āA�d�ʍ��̘a�� 0 �ł���h
���������Q�l�����ł͂������������ŁA���͂��ƌ��ꂵ���ł����A
���̐}�����Ă��������B
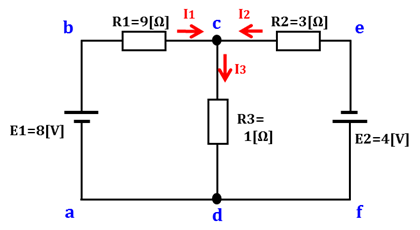
a�_�Ƃ����ꏊ������܂��B
�����̓d�ʂ��A���{���g�ł�������ł������Ɂu0V�v���Ƃ��܂��傤���B
�������炂�_�ւ����ƋN�d�͂��v���X���ꂽ�d�ʂɂȂ�A
b���炃�_�ɂ����ƒ�R�ɂ��d���~���iI1�~R1�j�œd�ʂ�������A
c���炄�_�ɍs���Ƃ����d���~���iI3�~R3�j�œd�ʂ�������A
������a�_�ɖ߂������ɂ́A�d�ʂ͌��́u0V�v�ɖ߂�܂���B
�Ƃ����Ă��邾���B
����_����o�����ĉ�H��������ƈ�������Ƃ��ɁA�o���_���������Ă܂��o���_�ɖ߂��Ă���킯�ł����A
�߂��Ă����Ƃ��ɓd�ʂ͕ς��܂����i�d�ʍ���0V�j�ƌ����Ă��邾���ł��B
��H��������Ă���ԂɁA�i�N�d�͂ɂ���āj�d�ʂ��オ������i�d���~���ɂ���āj�d�ʂ�����������͂��邯��ǂ��A
�o���_�ɖ߂����Ƃ��ɂ́A���̕����̓d�ʂ͕ς��܂���B
�Ƃ����A
��������@�����l�A������O�̂����������Ă���ɂ����܂���B
�u����A������Ă������Ƃ�����w���Ă��瓯���d�ʂł���I�v
���Ă��ƁB
������A����̉�H�Ɋ܂܂��N�d�͂Ɠd���~���A
�オ�������̓d�ʂ́A������Ă���ԂɕK�����������������A�Ƃ������ƂŁA
�N�d�͂̑��a �� �d���~���̑��a
�Ƃ����������ɂȂ�܂��B

�Ȃ̂ł��̉�H��a��b��c��d�Ƃ�����H�̏ꍇ���ƁA
�N�d�͂̑��a �� �d���~���̑��a
E1 �� I1R1 + I3R3
�Ƃ������ɂȂ�B
���Ȃ݂ɁA
�N�d�͂Ƃ����͓̂d�ʂ��オ��O��A�d���~���Ƃ����͓̂d�ʂ�������O��A
�ŏ�L�̂悤�ɐ����ɂ���̂ŁA
������H�����ǂ钆�ŁA�d�������ǂ�����ɑ��Ĕ��Ό����q�����Ă���
�u�N�d�͂�ʂ�̂ɓd�ʂ����������Ⴄ��I�v
���Ă����ꍇ�́A������������-E�ƂȂ�܂����A
�i��L��H���Af��e��c��d���Ă��ǂ�ƁAE2���t�������Ă���̂�-E2�ƕ\���j
��H�����ǂ�����ɑ��ēd�����t�����ɗ���Ă�
�u��R��ʂ�̂ɓd�����オ�����Ⴄ�v
�Ƃ����ꍇ�́A�d���~�����������ň����܂��B
�i��L��H���Af��d��c��e�Ƃ��ǂ�ƁAI3��I2�̓d�����������Ȃ̂ŁA-I3R3�A-I2R2�ƕ\���j
�L���q�z�b�t�̖@���Ƃ����̂͏�L�̎��������Ă邾���Ȃ̂ŁA����Ȃɓ�����̂���Ȃ��ł���ˁH
���ꂾ���Ȃ�ł���B
�u�L���q�z�b�t�̖@���v
�Ƃ����̂́B
�@�����̂͂������ȒP�A�Ƃ�������H���g������O�̎��h�������Ă��邾���̖@���ł��B
�ŁA���̃L���q�z�b�t�̖@���Ɋ�Â��ĉ�H���u�����v�ɂ��āA
�d���R��̖��ŏo�肳���p�^�[�����Ƃ��̐����ɂ������̂��g�A���������h�ʼn����킯�ł����A
�������T���l�������B
�ł�������āA
�L���q�z�b�t�̖@���������Ȃ��āA
�A���������������Ȃ������Ȃ����(/�ց_)
�Ȃ̂ŁA�L���q�z�b�t�̖@���������璲�ׂĂ�����͉������܂���B
�������邽�߂ɕK�v�Ȃ̂́A
�g�A���������̉������h
�ł��B
�A���������͒��Q���炢�ŏK�����e�Ȃ�Ȃ����Ǝv���܂������ʂɐ������Ă���A���������Ȃ�ĉ����Ȃ��̂ŁA�܂��Y�ꂿ�Ⴂ�܂����(^^;
�Ȃ̂ŁA�ȒP�ɂ����ŁA�d���R��ɕK�v�ȃ��x��������������Ă����܂��B
���Ⴀ�L���q�z�b�t�̖@�����g���ĉ�H�������Ă����܂��傤�B
�ł́A���̃y�[�W�ʼn��x���o�ꂵ�Ă��邱�̉�H�B

���́A
�uI3�ɗ����d��[A]�v
���A�L���q�z�b�t�̖@�����g���ĉ����Ă݂����܂��傤�B
�܂��́AR1�ɗ����d�����E������I1�AR2�ɗ����d������������I2�A�ƒ�`����Ă���̂ŁA
����_���ɒ��ڂ��đ��@����K�p����ƁA
I1+I2��I3
�Ƃ����������Ă��܂��B
���ɁA��H�� a��b��c��d��a �Ƃ������[�v�ōl���āA
����� ���N�d�́����d���~�� �Ƃ����`�Ő����ɂ��܂��B
E1��I1R1+I3R3
8��9I1+I3
����ɁA�E���ɂ܂����������Ă��Ȃ���H���c���Ă���̂ŁA
f��d��c��e�����@�Ƃ������[�v�œ����悤�ɐ���������ƁA
E2��-I3R3-I2R2
4��-3I2-I3
�i�d���̕������t�����ɂ��ǂ�̂œd���~���͕������ɂȂ�j
�������A���[�v�����ǂ�����́Af��e��c��d��f �Ə�L�Ƃ͔��̔����v�������ł��ǂ��Ă��A
-E2��I2R2+I3R3
-4��3I2+I3
�ƂȂ�܂����A���ϊ����ė��ӂ̕����]������A
4��-3I2-I3
�ƁA�S�������������ɂȂ�̂ŁA���ǂ�����Ɍ��܂�͂���܂���B
�͂��A�����܂ŁB
I1+I2=I3�@�E�E�E�@
8��9I1+I3�@�E�E�E�A
4��-I3-3I2�@�E�E�E�B
���̂R�ʼn�H��S�Ă��ǂ��āA��H�S�Ă𐔎����ł������ƂɂȂ�̂�
���Ƃ͂��̘A���������������킯�ł����A
�����ő�������ȋ^��B
�u���m�����R�������ĘA���������������Ȃ��I�v
�Ƃ����T����������l�������ł����A
���m�����R����Ȃ�A�܂��͂Q�ɍi��܂��傤�B
���̂��߂ɏ�L�̇@��������̂ł�����B
�������������@����Ƃ��Ď����܂��B
�A����I1�ɁA�@������ό`�ł���I1��I3-I2�������܂��B
8��9I1+I3
8��9�iI3-I2�j+I3
8��9I3-9I2+I3
8��10I3-9I2�@�E�E�E�A-2
�͂��A���̎��_�ŇB�ƇA-2����
I2��I3�����̂Q�̖��m���ɍi�ꂽ�̂ŁA�����A���������ʼn����܂��B
�A-2���ƇB�����������Ė��m�����������悤�ɂ��邽�߂ɁA
�B�����R�{����B
4��-I3-3I2�@�E�E�E�B
��
12��-3I3-9I2�@�E�E�E�B-2
����ŁA�A-2������B-2����������I2�������܂��B
�@�@8��10I3-9I2�@�E�E�E�A-2
�|�j12��-3I3-9I2�@�E�E�E�B-2
------------------
-4��13I3
I3��-4/13��-0.308[A]
�Ƃ������Ƃ�I3�̓d���l�����߂��܂���
�v�Z���ʂƂ��ă}�C�i�X�̒l�ɂȂ��Ă��܂��̂Ŏ��ۂ̓d���̗���́A��H�}�Œ�`���ꂽ�d���̕����i�������j�Ƃ͋t�����i������j�ɂȂ�Ƃ������Ƃł��ˁB
�܂�AI3�͍ŏ��������ɖ����`���Ă܂������A���ۂ̓d���͏������0.308A�����Ƃ������ʂɂȂ�܂��B
�Q�ȏ�̓d���������H���L���q�z�b�t�̖@����K�p���ĉ������Ƃ���Ɠd���̖��m�����R�ȏ�ɂȂ邱�Ƃ������āA�������T���l��������ł����A
�܂��͂������L�̂悤�ȉߒ��łQ�ɍi���Ă��������B
����ƁA�����@���g���Ăǂ��炩�̖��m�����������Ƃ��ł���̂ň�ɍi��A�ŏI�I�ɊȒP�Ȉꎟ�������̌v�Z�Ɏ������߂܂��B
���d�C��H�̉���͂�����������u���ł��s���Ă���̂Ő���Q�l�ɂ��Ă��������B
�֘A�L�� => �u�𗬓d�C�ȒP�ɍl������@�Ƃ́H�v
���X�X���y�[�W���� �u�������W�v
�����u���ւ̓o�^�͂������ςł����H
�l�i���i�Ƃ����Y�j�����͂������g�S�P�S��̓���u�`�h�������������Ō��J���I�ڍׂ͂�����̓�����������������B
�����u���ւ̓o�^�͂�����
https://wkmn-ytr.com/tsumekomi/
���m�点�i���i�Ƃ����Y�̍u���T�[�r�X�j
�����ɂ����Ȃ��g�w�K�̌��h�{���̒m����Nj������V�����d��3���̃I�����C���m�͂�����B
https://wkmn-ytr.com/daidenjuku/
�u�d���Q��͓���c�v�Ƃ����펯���I�����C���u���͂�����B
https://wkmn-ytr.com/2shusemi/